名词：FFT = Fast Fourier Transform（快速傅里叶变换）

      状态监控领域，将振动信号的时域波形转换为频域波形，常常用到傅里叶（FFT）变换。但是，可能有部分初涉该领域的从业人员对FFT并不是很了解，本文用实际例子对FFT做个数学方面的解释。

     我们知道，振动传感器安装在设备上时，它接收到的振动是该设备所有振动信号的叠加，传感器会把这些混叠信号毫无保留的传出，这些信号从示波器看上去杂乱无章，无法解读，因为示波器上显示的是时域波形，里面包含了多种频率的振动信号。

       那么，有没有一看就明白的信号显示方式呢？答案是：有。把时域信号转换为频域信号，就一目了然。而快速傅里叶变换（FFT）提供了实现从时域到频域的转换的工具。

       假如某台设备有2个振动信号：

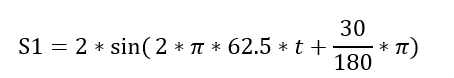
      即振幅为2g，频率为62.5Hz，相位为30度的信号（假设为主轴振动信号）。

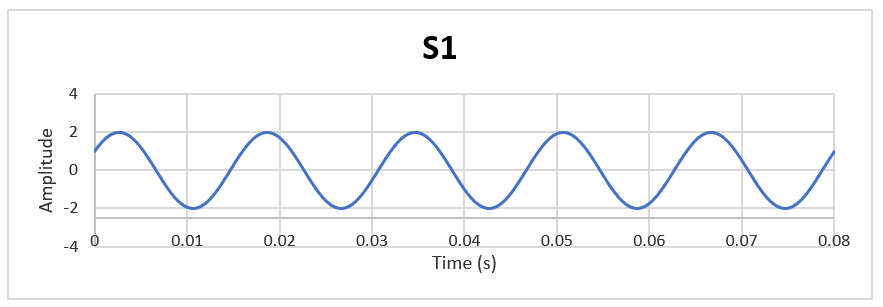
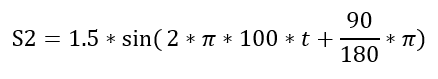
    即振幅为1.5g，频率为100Hz，相位为90度的信号（假设为此轮啮合振动信号）。

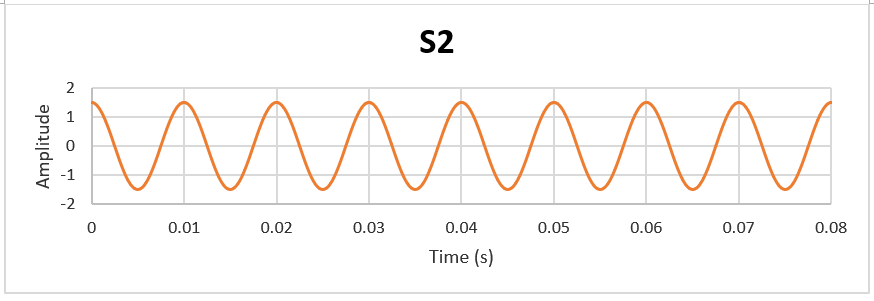
这2个信号都被森瑟科技 振动传感器310A接收到，并传给示波器，那么从示波器看到的波形就是这2个信号的叠加信号：S=S1+S2

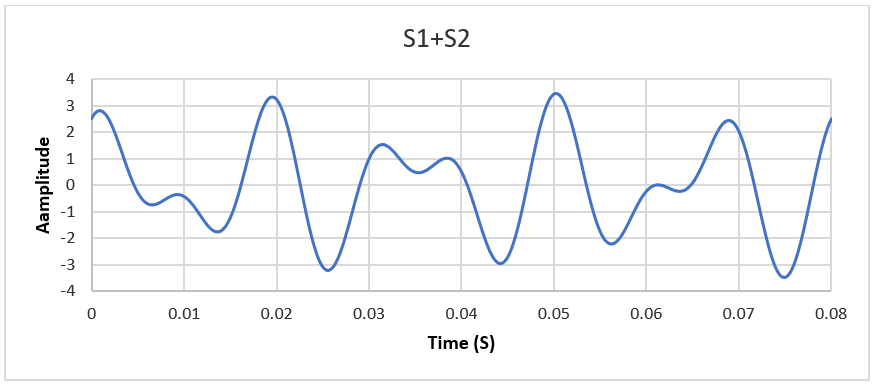
上图的这个波形是不是有点看不明白了呢？这才有2个信号叠加呢，3个叠加呢？10个叠加呢？100个呢？

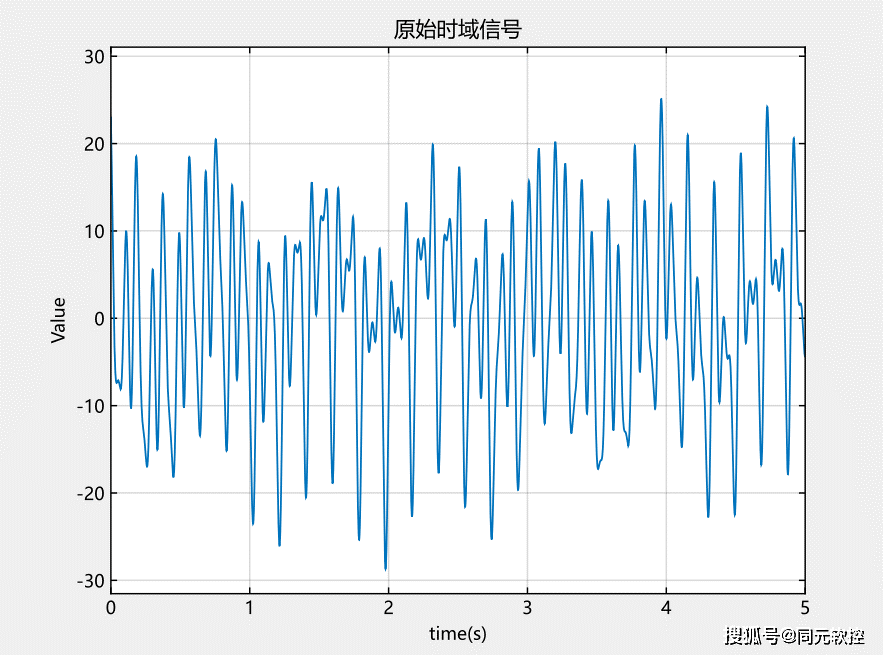
      完全看不明白了吧？不用理他，看下面包工怎么处理的。

      回归正传，此时，工程师（假设包工）并不知道上面是哪些信号的组合，包工需要把这些信号做FFT变换，得到时域信号才能知道是哪些频率组分的振动信号。通常，这个转换不需要包工自己来算，设备自带的数采就可以自行处理。为了读者理解，包工决定自己来算一算：

      第一步：包工用12800Hz的采样频率，在上述波形上采集了4096个数据（为什么是4096个数呢？尽量多，但是excel只能处理这么多），按照时间顺序，把这4096个数据写到excel表里，理论上，包工采到的每个点的数据就是S1和S2在该时间点的矢量和（S1+S2），如下表所示。虽然包工事先也不知道S1和S2，为便于读者理解，S1和S2的信息也列出。

    ...

     第二步：包工对这4096个数据进行FFT变换，这个工作在表格里用excel自带公式完成。得到如下数据：

     ...

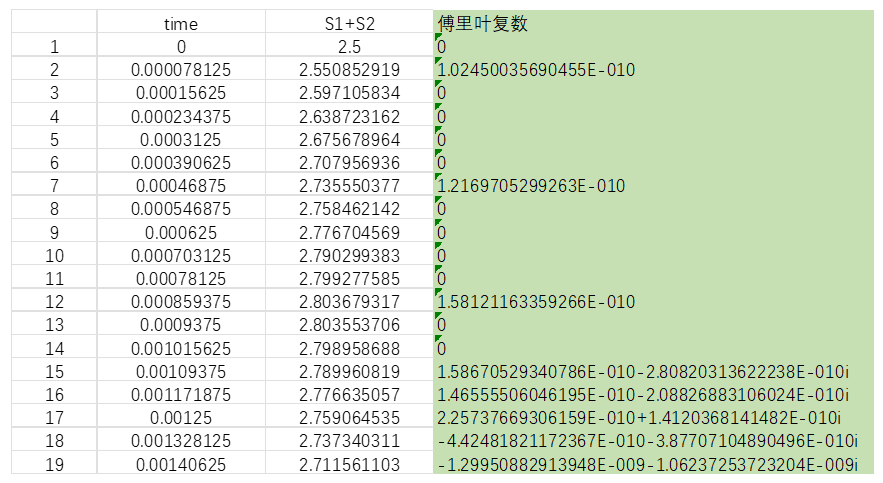
    第三步，包工对傅里叶复数进行频率化处理，这个得包工自己算:

1. 频数化，频率间隔 = 12800/4096 = 3.125 (Hz)，从公式看，采样频率越高，频率分别率越低呢，表示不解？提高采样时间和样本量，可以提高分辨率。低采样频率会导致混叠失真。

2. 求模（即振幅),和方根复数虚实部     (因为频域两侧对称能量减半，所以x2补偿回来)

数据如下：

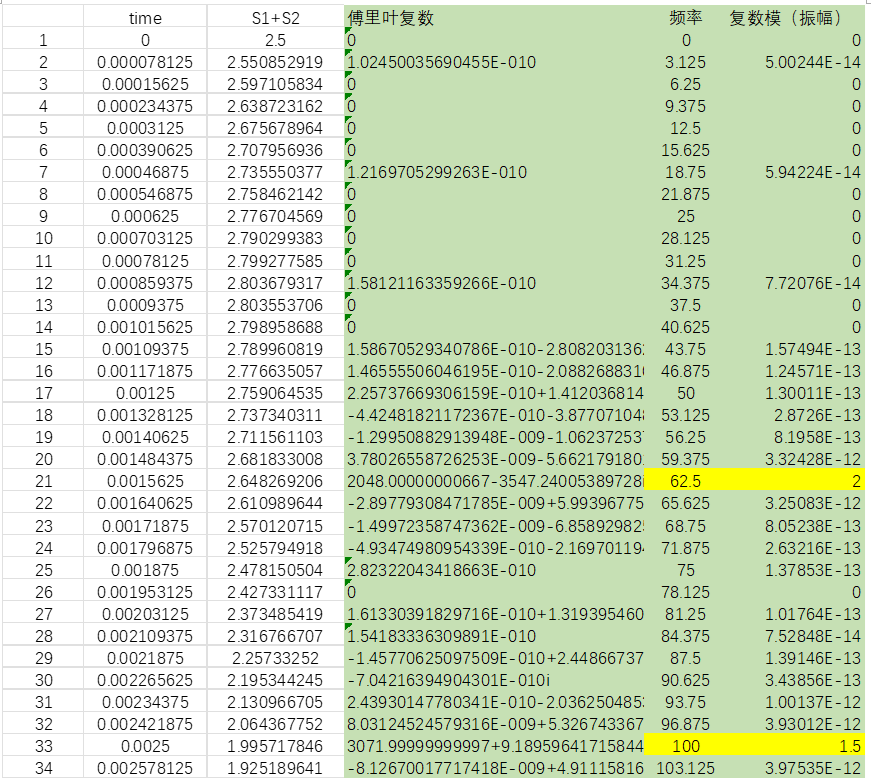
3.  绘制频谱图

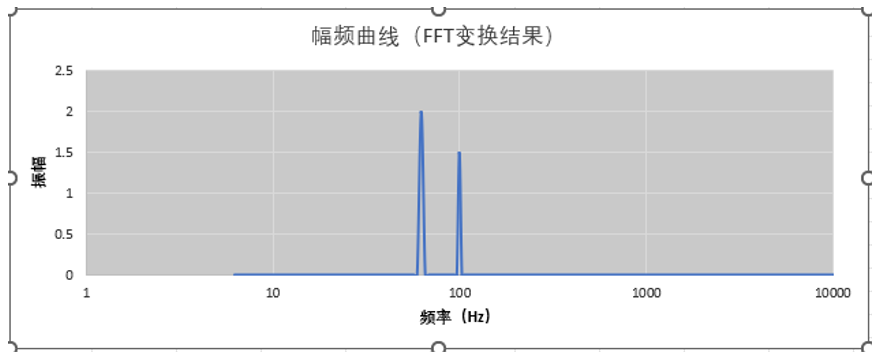
      从频谱图上，我们是不是看到62.5Hz处有个2g的振幅信号，在100Hz处有个1.5g的振幅信号呢？

      这，就是傅里叶变换。傅里叶变换是CMS振动分析的基础。

      一点历史知识：1807年法国数学家傅里叶(J. Fourier, 1768-1830)在向法国科学院呈交一篇关于热传导问题的论文中宣布了任一函数都能够展成三角函数的无穷级数，这就是后来傅里叶变化的理论基础。所有的周期信号都可以分解为有限个正弦信号和/或余弦信号的叠加，而所有的振动信号必然是周期信号，所以，所有振动信号都可以分拆为不同频率下的正弦/余弦信号，在频谱上直观呈现。