对于真实的振动系统，系统自身属性的非线性特性或者系统所受扰动的非线性特性是普遍存在的。不过在大多数工程问题中，往往可以将非线性因素近似简化为线性的，这种处理既简化了计算，同时又具有相当高的精度。但是对于某些问题，忽略非线性因素将会引起很大的误差，甚至导致求解的错误。例如，机翼的颤振问题，船舶在海浪中的大幅运动和系泊系统中系泊力的问题，高速列车的蛇形运动问题，都需要非线性振动的分析方法。尤其是随着科技水平的发展，机械和结构系统越来越复杂，运行环境越来越苛刻，非线性振动问题越发不容忽视。

在处理振动问题时，通常能够转化为数学上的微分方程问题。线性振动问题对应线性方程（组），而非线性振动问题则对应非线性微分方程（组）。当微分方程中出现未知函数及其一阶和二阶导数的非线性项时，方程称为非线性的。如：系统的恢复力是系统空间位置的非线性函数，阻尼力是系统运动或振动速度的非线性函数。

在线性振动中固有频率是很重要的概念，所谓“固有”，就在于它与初始条件、运动状态无关，是系统的固有属性。而对非线性系统来说，由于系统自由振动的频率与振幅有关，固有频率这个概念本身发生了很大变化。

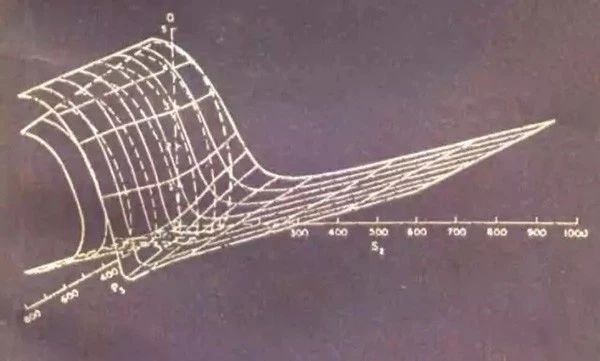
对于强迫振动问题，线性系统的响应频率必然与激励频率相同，但非线性系统的响应中有时异于激励频率的振动成分会很突出。幅频曲线在线性系统和在非线性系统中也大不相同，线性系统的幅频曲线是单值的，而非线性系统的幅频曲线在一个频率点可能对应若干振幅，即出现响应的多解情况。

在简谐激励作用下，线性系统的振动响应仍然为简谐振动，响应的大小与初始条件无关。但是非线性系统的响应与初始条件密切相关，由于初始条件的不同，其振动响应的发展将出现不同的结果，一个可能表现为周期的振动，而另一个则可能通向混沌运动。

对于多自由度系统，线性振动问题满足线性叠加原理，能够通过引入模态坐标将方程组解耦。而对于非线性振动问题，模态存在内共振、组合共振和各阶模态之间能量的渗透，因此，不可以用模态叠加的方法。虽然已有多种解析求解非线性振动的方法，包括多尺度法、三级数法、平均法、谐波平衡法等。但解析方法能够解决的问题很少，对于高维或强激励的问题便束手无策了，只能通过数值求解的方法，包括龙格-库塔法、有限差分法、Houbolt法、纽马克-β法、威尔逊-θ法等。

版权声明，部分图片文章来源网络，如有侵权，请通知网站删除更新处理！